Sistemi di numerazione e… rastrelli!
Un sistema di numerazione associa le diverse quantità (come: zero, uno, due, tre ecc.) ad un insieme di simboli (come: 0, 1, 2, 3 ecc.).
Il sistema che usiamo ogni giorno è detto decimale (o a base 10). Come tutti i sistemi di cui parleremo è un sistema posizionale: ciò vuol dire che lo stesso simbolo ha un significato diverso, in termini di quantità, a seconda della posizione che occupa (ad esempio nel numero 12 la cifra 1 indica la quantità dieci, mentre nel numero 21 la cifra 1 indica la quantità uno).
Il sistema a base 10
Nel sistema decimale sono disponibili 10 cifre (da 0 a 9) ed è detto a base 10 perché, per conoscere il significato delle cifre, queste vanno moltiplicate per le potenze a base 10. La cifra più a destra va moltiplicata per 100 (le unità), la cifra nella posizione precedente va moltiplicata per 101 (le decine), la cifra precedente va moltiplicata per 102 (le centinaia) e così via. Ad esempio il numero 153 è formato da 100+50+3 ossia 1×102+5×101+3×100.
Con il medesimo metodo, cambiando la base, gli stessi simboli possono avere significato diverso in termini di quantità. Nel seguito parliamo del sistema binario (perché legato alla scienza dell’informazione e al funzionamento dei computer) e del sistema esadecimale (perché chi si occupa di informatica lo incontrerà in diverse situazioni).
Il sistema a base 2
Nel sistema binario (o a base 2) sono disponibili due sole cifre (0 e 1) e per conoscere il significato delle cifre, queste vanno moltiplicate per le potenze a base 2. La cifra più a destra va moltiplicata per 20, la cifra nella posizione precedente va moltiplicata per 21, la cifra precedente va moltiplicata per 22 e così via. Ad esempio il numero 1012 corrisponde a 1×22+0x21+1×20=410+0+110=510.
Il sistema a base 16
Nel sistema esadecimale (o a base 16), le cifre disponibili sono 16 (da 0 a 9 e da A a F). Per conoscere il significato delle cifre, queste vanno moltiplicate per le potenze a base 16. La cifra più a destra va moltiplicata per 160, la cifra nella posizione precedente va moltiplicata per 161 e così via. Ad esempio il numero 1A16 corrisponde a 1×161+Ax160 ossia a 1×16+10×1=2610 (visto che il simbolo A corrisponde alla quantità dieci).
I rastrelli
Per passare agevolmente da una base all’altra esistono diversi metodi e sicuramente usare la calcolatrice del proprio smartphone è il più comodo 🙂
Qui però vediamo un metodo (che io chiamo “dei rastrelli rovesci”) per il calcolo manuale, per quantità intere comprese fra 0 e 255.
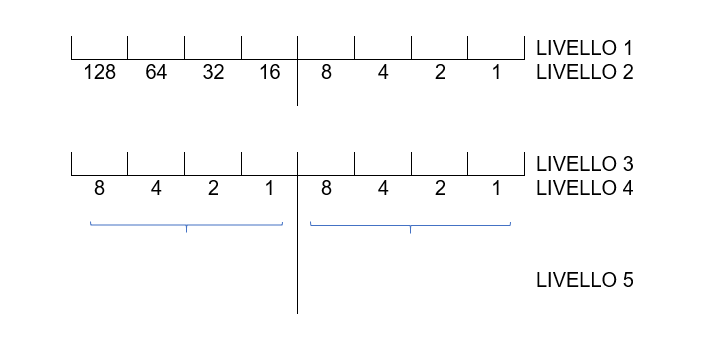
1) Disegnamo una struttura come quella in figura
2) Riportiamo le serie di numeri indicate, che corrispondono rispettivamente alle prime 8 potenze a base 2 (livello 2) e alle prime 4 potenze a base 2 (livello 4)
A questo punto ci muoviamo diversamente, a seconda della conversioni fra basi che vogliamo fare.

A) DA DECIMALE A BINARIO
Esempio: convertire il numero 13810 da decimale a binario.
– scomporre il numero in somma di numeri al livello 2 (138=128+8+2)
– al livello 1 scrivere la cifra 1 in corrispondenza di ogni numero del livello 2 che si è utilizzato
– al livello 1 scrivere la cifra 0 in corrispondenza di tutti gli altri numeri del livello 2 non utilizzati
Risultato ottenuto: 13810=100010102
B) DA BINARIO A DECIMALE
Esempio: convertire il numero 100010102 da binario a decimale.
– scrivere le cifre componenti il numero al livello 1
– addizionare i numeri del livello 2 corrispondenti alle cifre 1 scritte al livello 1 (128+8+2=138)
Risultato ottenuto: 100010102=13810
C) DA BINARIO A ESADECIMALE
Esempio: convertire il numero 100010102 da binario a esadecimale
– scrivere il numero 10001010 al livello 3
– addizionare i primi quattro numeri del livello 4 corrispondenti alle cifra 1 scritte al livello 3
– la somma risultante va scritta sul lato sinistro del livello 5, al centro, considerando che deve essere costituita da una unica cifra (nel nostro caso risulta 8 quindi la scriviamo così)
– addizionare i secondi quattro numeri del livello 4 corrispondenti alle cifra 1 scritte al livello 3
– la somma risultante va scritta sul lato destro del livello 5, al centro, considerando che deve essere costituita da una unica cifra (nel nostro caso la somma risulta 8+2=10 quindi scriviamo A, ricordando che nel sistema esadecimale A=dieci, B=undici, C=dodici, D=tredici, E=quattordici, F=quindici)
Risultato ottenuto: 100010102=8A16
D) DA ESADECIMALE A BINARIO
Esempio: convertire il numero 8A16 da esadecimale a binario
– scrivere al livello 5 (una per lato) le due cifre componenti il numero da convertire
– scomporre ciascuna cifra nella somma dei numeri al livello 4, riportando al livello 3 la cifra 1 in corrispondenza dei numeri utilizzati, 0 altrimenti (nell’esempio si scriverà da sinistra a destra: 10001010, dato che si è usato un 8 per a sinistra e si sono usati un 8 e un 2 a destra)
E) DA ESADECIMALE A DECIMALE
– fare i passi al punto D)
– fare i passi al punto B)
F) DA DECIMALE A ESADECIMALE
– fare i passi al punto A)
– fare i passi al punto C)
Beh. Forse è più agevole vedere un video che lo spiega.
Bibliografia: Rossignoli, N., Introduzione al digitale, Lampidistampa, Milano, 2007
Immagine: Photo by Nicola Rossignoli presso Liceo Maffei – Verona



